Using a Genetic Algorithm to Guess Arithmetic Equations in Julia

Genetic algorithms try to replicate the mechanisms of biological evolution to solve problems. In this article we'll use a somewhat useless example problem to demonstrate how to design and implement a genetic algorithm in Julia which I have been trying to learn recently.

Taking the example of the expression 4 * 9 / 2 + 5 - 3, we would normally want to get the result of evaluating this expression. However, for our purposes it is much more interesting to start off with a result and try and find an expression that returns that result when evaluated. So for our example we'd start with 20 then try and find an expression such as 4 * 5.

Evolution, what's that?

Before we can jump into writing code, it may be useful to understand at least some of the underlying ideas behind the functioning of genetic algorithms key of which is evolution. It is described on WikiPedia as:

the change in the heritable characteristics of biological populations over successive generations. Evolution occurs when evolutionary processes such as natural selection and genetic drift act on genetic variation, resulting in certain characteristics becoming more or less common within a population over successive generations.

In general the more beneficial a certain trait is for survival, the more likely it is to for organisms carrying it to survive long enough to pass on their genes. This leads to the trait becoming more common in a population during successive generations. This process is natural selection which was the primary inspiration for genetic algorithms.

Genetic Algorithms

Genetic algorithms are commonly used on problems where finding solutions through more direct means is too resource intensive to be feasible, for example scheduling. They typically have a few key steps:

1. Generating a random start population.
2. Selecting candidates for producing the next generation.
3. Using crossovers and mutations to create a new generation from the selected parents.
4. Checking if a solution has been found and terminating or going back to step 2.

Each of the first 3 steps can vary in many different ways and how exactly you do each could influence the performance of the final algorithm as a whole. I'll try and keep things simple but I'll try to point out places where you could change things up for anyone interested in exploring alternate approaches.

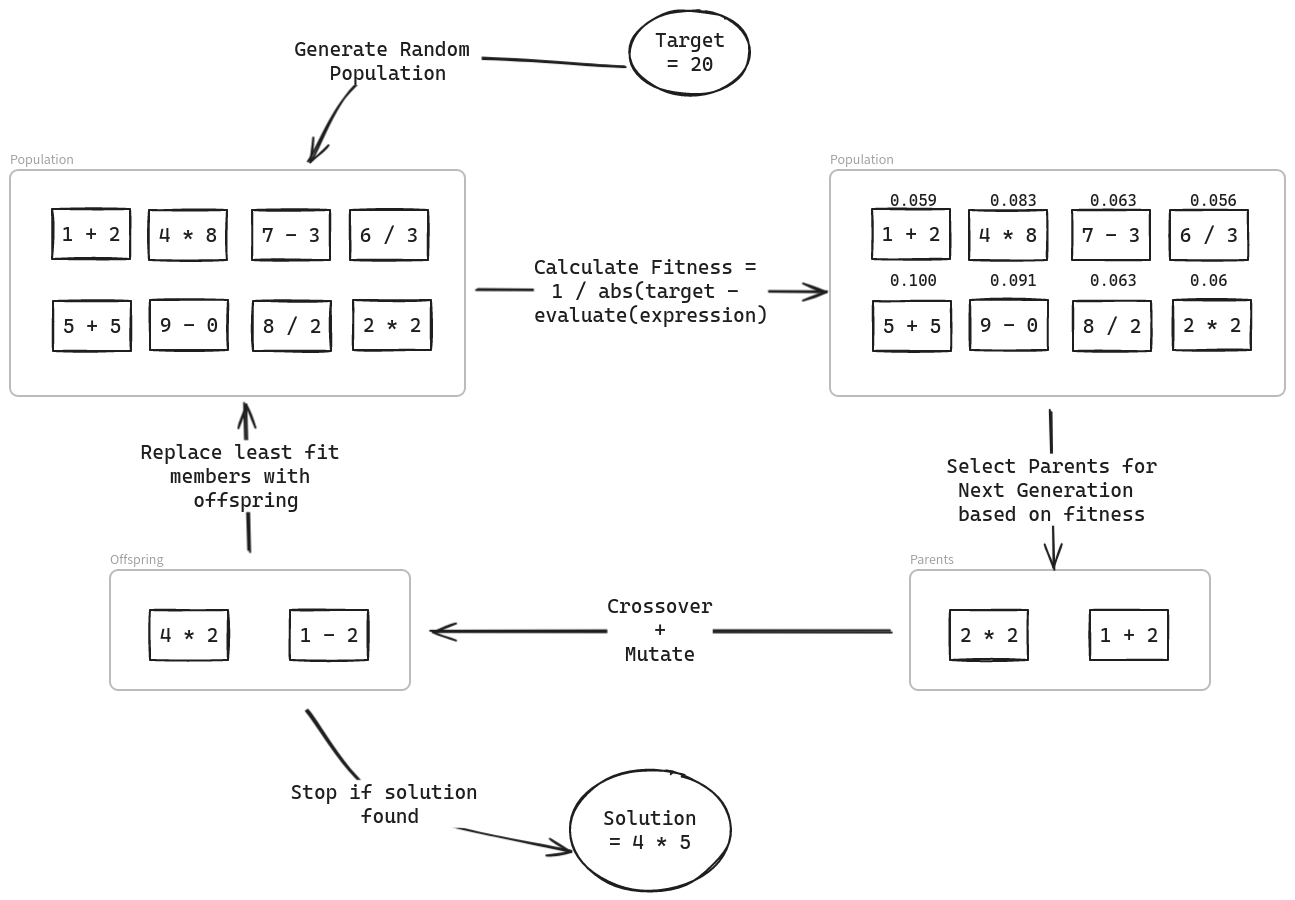
Translating the Problem into code

There's a lot more involved in genetic algorithms than just 4 steps. The first thing we have to do is phrase our problem adequately. We need to figure out what constitutes a population and how are traits in each member represented so they can be "passed on". Keep in mind what we're trying to do with the genetic algorithm is evolve the population until one of the members fit the solution we are trying to find.

In this case a population would be a bunch of arithmetic expressions so it would have members like 3 + 7 * 4, 9 / 1 - 4, 8 etc. More concretely an expression would contain any number from 0 to 9 and the operators *, /, + and -. There's the additional constraint that an expression can only be 9 terms long which is enough for each of the 4 operators to be used once. This constraint is mostly just for simplicity's sake so there's no reason you couldn't allow for longer expressions. Expressions are in the form of a single number optionally followed by groups of operand and operator i.e [0-9]([+-*/][0-9])*.

We'll take the entire expression as a chromosome and split each term into individual genes. With a total of 14 possible options for each gene we need at least 4 bits (ceil(log2(14)) = 4) to uniquely represent each gene. With 9 genes per expression that works out to 36 bits total.

In our implementation we'll use a 64bit unsigned integer which can hold a chromosome with room to spare. It is less likely that real world problems would require so few bits so bit arrays are commonly used instead of integers since they also support the bitwise operators necessary for crossover and mutation operations but can be larger.

To make our lives easier and also because Julia has great support for working in arrays, we'll have two alternate representations for expressions:

• An array of unsigned integers with each element corresponding to a gene.
• A single 64bit unsigned integer with every 4 bits being a gene.

Let's define these two representations along with methods to convert between them.

const GENE_SIZE = 4
const EXPRESSION_LENGTH = 9
const CHROMOSOME_SIZE = GENE_SIZE * EXPRESSION_LENGTH

Expression = Vector{UInt64} # unsigned integer technically only needs to be 4 bits
EncodedExpression = UInt64


expression_chars =
    ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '+', '-', '*', '/']

function encode(expression::Expression)::EncodedExpression
    res = EncodedExpression(0)
    for i in expression
        res <<= GENE_SIZE
        res |= i
    end
    return res
end

function decode(expression::EncodedExpression)::Expression
    expr = []
    expr_mask = (1 << GENE_SIZE) - 1
    for _ in (1:EXPRESSION_LENGTH)
        v = expression & expr_mask
        pushfirst!(expr, v)
        expression >>= GENE_SIZE
    end
    return expr
end

Base.convert(::Type{EncodedExpression}, x::Expression) =
    encode(x)
Base.convert(::Type{Expression}, x::EncodedExpression) =
    decode(x)

The encode functions takes a vector of genes (Expression) and crams them all into a single unsigned 64bit integer (EncodedExpression). decode does the reverse and extracts every 4 bits from said integer back into a vector. A Vector in Julia is a one-dimensional array.

We define also add methods to Base.convert to make translating between the two representations easier. Instead of needing to keep track of whether to call encode or decode, we can just call convert with the type we want and the value we want to convert.

Now that we have a data representation for expressions, it would be nice to have a nice way to create expressions.

function make(str::String)::Expression
    e = []
    # remove '=' and anything that follows
    str = first(split(str, "="))
    for i in str
        if !(i in expression_chars)
            continue
        else
            push!(e, findfirst(isequal(i), expression_chars) - 1)
        end
    end
    return e
end

make("1 + 2")

3-element Vector{UInt64}:
 0x0000000000000001
 0x000000000000000a
 0x0000000000000002

From the above code we can see that the value of each character in the expression is equal to one less than it's index in the expression_chars vector. This makes it easy to map between the programmatic and mathematical representation of numbers. Based on this mapping we can check that numbers are valid if they are between 0 and 9. Similarly operators are valid when they are between 10 and 13. Let's write a function to check that an expression datatype is correct.

isnumber(x) = x >= 0 && x <= 9
isoperator(x) = x >= 10 && x <= 13

function isvalid(expression::Expression)
    nums = [expression[i] for i in (1:2:length(expression))]
    ops = [expression[i] for i in (2:2:length(expression))]
    return all(isnumber, nums) && all(isoperator, ops)
end

function isvalid(expression::EncodedExpression)
    return isvalid(convert(Expression, expression))
end

It sometimes may be more convenient to define a function on Expression or EncodedExpression but since we still want the function to work with either type, we use convert to first transform the argument before calling the function we defined. I don't know if this is an anti-pattern but I found it pretty cool and made figuring out the various functions a lot easier. For subsequent functions I'll leave out definitions that just do a conversion but they're still present in the complete code.

Generating A Random Start Population

To create a start population we need to be able to generate random valid expressions.

function random_expression(; num_terms = nothing)::Expression
    num_terms = isnothing(num_terms) ? rand(1:2:EXPRESSION_LENGTH) : num_terms
    num_terms % 2 == 0 &&
        num_terms <= EXPRESSION_LENGTH &&
        error("num_terms must be odd number")
    expression = []
    for i in (1:num_terms)
        if i % 2 != 0
            push!(expression, rand(Vector(1:9)))
        else
            push!(expression, rand(Vector(10:13)))
        end
    end
    return expression
end

isvalid(random_expression())

true

I had initially set this function to always generate an expression of maximum length but decided to instead pick a random length. The thought process was that longer expressions had more active (non-empty) genes hence more genes for crossover and mutation. However, this meant that the overall population would be less diverse making it harder to arrive at a solution due to the population being too similar.

Next is a function that shows a human-readable representation of expressions.

function showexpression(expression::Expression)
    if isempty(expression)
        return "empty expression"
    end
    return join([expression_chars[i+1] for i in expression], " ")
end

function showexpression(expression::EncodedExpression)
    return showexpression(convert(Expression, expression), show_result)
end

showexpression(random_expression(num_terms = 9))

"1 + 6 * 6 * 5 + 6"

Pretty simple thanks again to being able to treat expressions as vectors. Finally we can define the function to generate a random population.

createpopulation(population_size = 100)::Vector{EncodedExpression} = map(
    Base.Fix1(convert, EncodedExpression),
    [random_expression() for _ in (1:population_size)],
)

We call convert through Base.Fix1 whose usage is explained in the documentation as:

Fix1(f, x) A type representing a partially-applied version of the two-argument function f, with the first argument fixed to the value "x". In other words, Fix1(f, x) behaves similarly to y->f(x, y). See also Fix2.

Selecting Candidates for Producing the Next Generation

To produce the next generation we need to pick two "parents" from the current generation's population according to their fitness. How do we do this? Well, first we need to figure out how close a particular solution is to our desired result. Since we're looking for an expression that evaluates to a particular value, we need to first be able to evaluate expressions. Before we do this though we need to take a little detour.

Over the course of our program, we are likely to have expressions that are not strictly well-formed. However, instead of discarding the entire expression once isvalid is false, it would be better if we could try and process the expression into a valid one whenever possible. This means that an expression like 1 + + 5 * 8 3 / 4 which is invalid would be turned into 1 + 5 * 8 / 4 which is well-formed according to our previous rules.

To do this we need to check:

• that each entry in an expression is either a number or operator.
• that each number and is followed by an operator or nothing and each operator is followed by a number.

We do this using isnumber and isoperator defined previously together with a boolean flag that keeps track of whether we should expect a number next to build a new expression.

function clean(expression::Expression)::Expression
    if isvalid(expression) || isempty(expression)
        return expression
    end
    expression = copy(expression)
    num = true
    result = []
    for i in expression
        if isnumber(i) && num
            push!(result, i)
            num = !num
        elseif isoperator(i) && !num
            push!(result, i)
            num = !num
        end
    end
    if num
        pop!(result)
    end
    return result
end

showexpression(clean(make("1 + + 5 -")))

"1 + 5"

Since we're working with arrays we use copy just so we don't end up mutating the original argument which may be needed unmodified outside our function.

Using clean we can make our evaluation function much simpler since we don't need to include extra error handling for malformed expressions. Keep in mind that we evaluate expressions in left to right order with all operators having equal precedence.

function evaluate(expression::Expression)
    expression = clean(expression)
    result = Float64(popfirst!(expression))
    while !isempty(expression)
        o = popfirst!(expression)
        l = popfirst!(expression)
        if '*' == expression_chars[o+1]
            result *= l
        elseif '/' == expression_chars[o+1]
            result /= l
        elseif '+' == expression_chars[o+1]
            result += l
        elseif '-' == expression_chars[o+1]
            result -= l
        end
    end
    return result
end

function evaluate(expression::EncodedExpression)
    return evaluate(convert(Expression, expression))
end

evaluate(make("1 + 5"))

6.0

For a fitness function we need the output to be larger the input is to our target value.

function fitness_score(expression, target)
    if isempty(expression) || iszero(expression)
        return 0
    end
    return 1 / abs(target - evaluate(expression))
end

fitness_score(make("2 * 8"), 10)

0.16666666666666666

The right fitness function is dependent on what type of problem you're trying to solve and even for our specific example there may be a better one. Try and figure out a better one if you can and let me know in the comments.

We don't need to worry about divide by zero errors in Julia but we'd need to check for this is we were using Python for instance. This works out nicely since the fitness score for an expression matching our target is Infinity.

To actually select candidates for producing the next generation we need to use fitness proportionate selection aka roulette wheel selection. This function is is defined as

$$p_ = \frac{f_}{\sum_^f_}$$

In simple terms this means that the probability of selecting a particular member of the population $i$ is equal to it's fitness divided by the sum of all the fitness scores for the entire population. Translating this to Julia can be done easily by using the sample function from the StatsBase.jl package which allows random selection based on provided probability weights.

using StatsBase: sample, Weights

function roulette_wheel(fitness, population, size = 2)
    weights = fitness / sum(fitness)
    return sample(population, Weights(weights), size, replace = false)
end

fitness is an array containing the fitness scores of the members in population in the same order. (fitness = fitness_score.(population)). size tells sample how many randomly selected items we want which saves us the effort of calling this function twice to find each 'parent'. We also pass replace = false to make sure that we do not return the same members of the population for our selection.

Genetic Operators: Crossover & Mutation

Up-to this point other than the data representation there's not much resemblance to natural selection in biology. We could a write a function go

function go(N = 100, n = 50, t = 20)
  population = create_population(N)
  fitness = fitness_score.(population, t)
  while !(Inf in fitness)
    fittestn = roulette_wheel(fitness, population, n)
    population = vcat(fittestn, create_population(N - n))
    fitness = fitness_score.(population, t)
  end
  return findfirst(isinf, population)
end

Although we could in theory find a solution this way, whether or not this function returns in a reasonable time is impossible to tell. Crossovers and mutations help improve our chances of finding a solution in a reasonable time frame by mimicking nature.

• Crossover swaps the bits of two chromosomes starting a random point similar to how genes combine during reproduction.
• Mutation randomly flips a bit in a chromosome. It serves the purpose of retaining the genetic diversity of a population. When the members of a population become too similar to each other it slows down the convergence towards a solution as mentioned before.

There are other genetic operators as well as different variations for crossover and mutation but we'll keep things simple for now. Here's crossover:

const CROSSOVER_RATE = Float64(0.5)

function crossover(
    e1::EncodedExpression,
    e2::EncodedExpression,
    rate::Float64 = CROSSOVER_RATE,
)
    if rand(Float64) <= rate
        e1 = copy(e1)
        e2 = copy(e2)
        position = rand(1:CHROMOSOME_SIZE-1)
        mask = EncodedExpression(0)
        for i = 0:position
            mask |= (EncodedExpression(1) << i)
        end
        complement = ~mask

        c1_bits = e1 & mask
        c2_bits = e2 & mask

        r1 = e1 & complement
        r2 = e2 & complement

        r1 |= c2_bits
        r2 |= c1_bits
        return (r1, r2)
    else
        return (e1, e2)
    end
end

Both crossover and mutation are only performed according to some predefined rate. There isn't really a 'correct' value for these rates so you'd probably have to try different values and find what works for your particular problem or even just for this one.

Crossover swaps bits by creating a mask and extracting the bits in the required positions for each number before ORing them in swapped order.

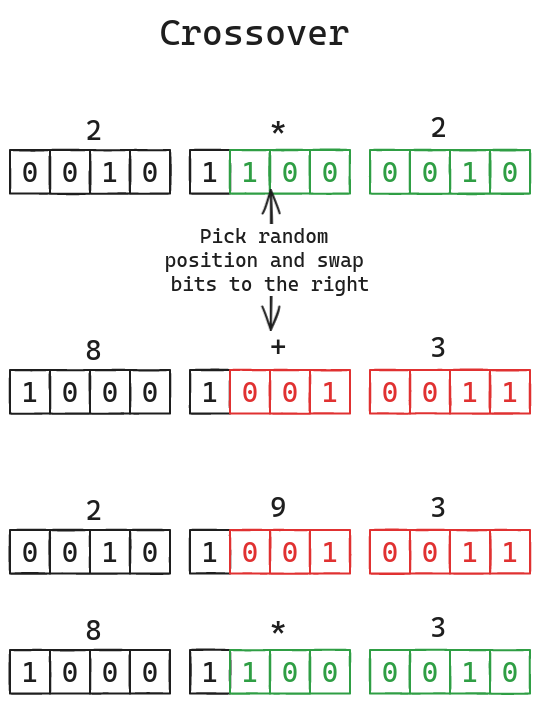
const MUTATION_RATE = Float64(0.01)

function mutate(expression::EncodedExpression, rate::Float64 = MUTATION_RATE)
    if rand(Float64) <= rate
        expression = copy(expression)
        position = rand(1:CHROMOSOME_SIZE)
        mask = 1 << position
        return xor(expression, mask)
    else
        return expression
    end
end

Mutation also involves creating a mask, but this time we simply XOR the chromosome with the mask to flip a bit at a randomly selected position. Since both these functions operate on bits let's make a function to show expressions as bit strings grouped into individual genes.

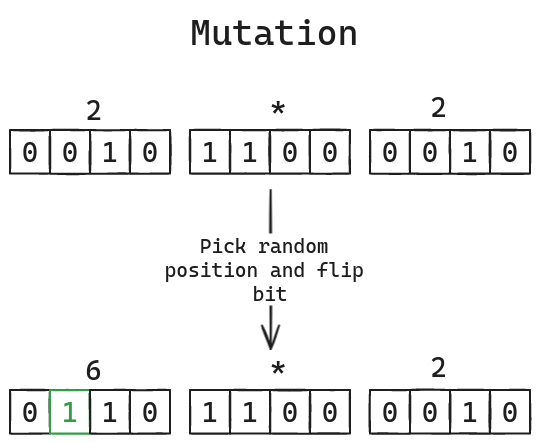
asbitstring(expression::EncodedExpression) =
    string(expression, base = 2, pad = CHROMOSOME_SIZE)

function showencoding(expression::EncodedExpression)
    bitstr = asbitstring(expression)
    n = length(bitstr)
    formatted_bitstr = String[]

    for i = 1:GENE_SIZE:n
        push!(formatted_bitstr, bitstr[i:min(i + (GENE_SIZE - 1), n)])
    end
    return join(formatted_bitstr, ' ')
end

showencoding(0x00000007c6a8d3b6)

"0111 1100 0110 1010 1000 1101 0011 1011 0110"

Putting it all together

We now have all the essential parts for making our genetic algorithm work but there's two more things we can add to improve the UX of our program. The first is a progress meter so we can keep track of how our things are going, and also some way to store the results of each run. The latter especially is important if we want to asses how different variations affect the performance of our program.

For progress ProgressMeter.jl is trivial to use and has a bunch of useful features. For saving data I'm partial to SQLite mostly because Python - which is the language I use most - supports it in the stdlib but also because it is file based which simplifies using SQL a lot. The SQLite.jl package is necessary to use SQLite in Julia.

As an aside anyone with a good recommendation for a file-based document database leave it in the comments please.

The statistics we want to collect are:

• Which target were we trying to find an expressions for.
• The solution if one has been found.
• The population at the time the algorithm terminates. It may also be useful to collect the population for each generation but we'll leave that out for now.
• How many generations have been run before terminating.
• The total number of generations that can be run.
• How many mutations have been done.
• How many crossovers have been done.

Most of these map easily to SQL datatypes except the population which is a vector of expressions. For this field the simplest option was to use the JSON type in SQLite. We also use showexpression to get the human-readable version of each expression just so the database file is less tightly coupled to the expression datatype we choose.

CREATE TABLE IF NOT EXISTS experiment_stats (
  id INTEGER PRIMARY KEY AUTOINCREMENT,
  target REAL UNIQUE NOT NULL,
  population_size INTEGER NOT NULL,
  max_generations INTEGER NOT NULL,
  generations_run INTEGER NOT NULL,
  mutations INTEGER NOT NULL,
  crossovers INTEGER NOT NULL,
  solution TEXT,
  population JSON NOT NULL,
);

After defining the table required to store statistics we can write a function for storing them.

using SQLite;
using JSON;

db = SQLite.DB("data.db")

function savestats(stats)
    stats[:population] = JSON.json(map(showexpression, stats[:population]))
    stmt = DBInterface.prepare(
        db,
        """
        INSERT INTO experiment_stats (
            target, 
            population_size,
            max_generations,
            generations_run,
            mutations,
            crossovers,
            solution,
            population
        ) VALUES (
            :target,
            :population_size,
            :max_generations,
            :generations_run,
            :mutations,
            :crossovers,
            :solution,
            :population
    )
    """,
    )
    res = DBInterface.execute(stmt, stats)
    DBInterface.close!(stmt)
    return res
end

stats is a Dict with the keys :target, :population_size, :max_generations, :generations_run, :mutations, :crossovers, :solution and :population.

Last but not least we define the function that puts everything together into the genetic algorithm.

using ProgressMeter;

function ga(;
    target = 20.0,
    population_size = 1000,
    max_generations = 500,
    show_progress = true,
    save_results = true
)
    population = createpopulation(population_size)
    fitness = fitness_score.(population, target)
    stats = Dict{Symbol,Union{Nothing,Real,String,Vector{UInt64}}}(
        :target => target,
        :population_size => length(population),
        :max_generations => max_generations,
        :generations_run => 1,
        :mutations => 0,
        :crossovers => 0,
        :solution => nothing,
        :population => nothing,
    )
    prog = ProgressUnknown(
        "Searching for solution to $(target):",
        spinner = true,
        enabled = show_progress,
    )
    # check if solution already exists in population and exit early
    if Inf in fitness
        e = population[findfirst(isinf, fitness)]
        ProgressMeter.finish!(prog)
        println("found solution for $(target): ", showexpression(e))
        stats[:solution] = showexpression(e)
        stats[:population] = population
        save_results && savestats(stats)
        return stats[:solution]
    end

    for g in (1:max_generations)
        for _ in (1:population_size)
            ProgressMeter.next!(
                prog,
                showvalues = [
                    (:generations_run, stats[:generations_run]),
                    (:mutations, stats[:mutations]),
                    (:crossovers, stats[:crossovers]),
                ],
            )
            p1, p2 = roulette_wheel(fitness, population, 2)

            e1, e2 = crossover(p1, p2)
            e1, e2 = mutate(e1), mutate(e2)

            f1, f2 = fitness_score(e1, target), fitness_score(e2, target)
            if isnan(f1) || isnan(f2)
                continue
            end
            stats[:crossovers] += e1 == p1 ? 0 : 1
            stats[:mutations] += e1 == p1 ? 0 : 1
            stats[:mutations] += e2 == p2 ? 0 : 1

            # check if either offspring is solution
            for e in [e1, e2]
                if isinf(fitness_score(e, target))
                    e = clean(e)
                    ProgressMeter.finish!(prog)
                    println("found solution for $(target): ", showexpression(e))
                    stats[:solution] = showexpression(e)
                    stats[:population] = population
                    save_results && savestats(stats)
                    return
                end
            end
            
            # replace least fit members with new offspring with better fitness
            least_fit = argmin(fitness)
            population[least_fit] = f1 < f2 ? e1 : e2
            fitness[least_fit] = f1 < f2 ? f1 : f2
        end
        stats[:generations_run] = g
    end
    stats[:population] = population
    save_result && savestats(stats)
end

ga(;target = 30, population_size=1000, max_generations=100, save_results = false)

found solution for 30: 2 * 3 * 5 * 9 / 9

"2 * 3 * 5 * 9 / 9"

Looks pretty cluttered. If we ignore all the parts that are not necessary for the genetic algorithm we get:

function ga(; target = 20.0, population_size = 1000, max_generations = 500)
    population = createpopulation(population_size)
    fitness = fitness_score.(population, target)
    # check if solution already exists in population and exit early
    if Inf in fitness
        e = clean(population[findfirst(isinf, fitness)])
        println("found solution for $(target): ", showexpression(e))
        return e
    end

    for g in (1:max_generations)
        for _ in (1:population_size)
            p1, p2 = roulette_wheel(fitness, population, 2)

            e1, e2 = crossover(p1, p2)
            e1, e2 = mutate(e1), mutate(e2)

            f1, f2 = fitness_score(e1, target), fitness_score(e2, target)
            if isnan(f1) || isnan(f2)
                continue
            end

            # check if either offspring is solution
            for e in [e1, e2]
                if isinf(fitness_score(e, target))
                    e = clean(e)
                    println("found solution for $(target): ", showexpression(e))
                    return e
                end
            end
            
            # replace least fit members with new offspring with better fitness
            least_fit = argmin(fitness)
            population[least_fit] = f1 < f2 ? e1 : e2
            fitness[least_fit] = f1 < f2 ? f1 : f2
        end
    end
end

All that's left is to try out our example with a few examples and see how it does. From my exploration, with the default arguments to ga we were unable to find a solution for numbers greater than 5000 more than 10% of the time. For numbers lower than 5000 the percentage was a considerably higher. That closes out our exploration of genetic algorithms.

Final Thoughts

• The idea for this project can from this article. It has implementations of the same problem in different languages. I tried this out about 5 years ago while learning C. It was a big nightmare but was the only non-trivial C project I completed outside some stuff with flex and bison.
• Really liking Julia so far. I've barely scratched the surface of it's capabilities. I'm especially looking forward to trying Makie. Anyone with tips on how to improve my Julia game leave them in the comments.
• Not usually a fan of YouTube videos for learning programming but I recommend the doggo dot jl channel for getting introduced to Julia.
• I wrote most of this using Quarto. Need to try it more before I can give a verdict.
• I would like explore other optimization algorithms like Hill climbing and Simulated Annealing as well as try make a few simulations. Recently watched a great video about fluid simulation.
• Haven't even tried to make this program go fast yet which is something you'd have to do if you wanted to use genetic algorithms in real life. Speed is also one of Julia's main selling points.
• We collect data from runs of our program but don't do anything with it. I already started work on this and should be write a follow up article soonish.
• Here is the repo with the entire code.